
One of the most vital uses of potential flow theory was the analysis of lifting surfaces such as the wings of an aircraft, since the boundary conditions on a complicated geometry can substantially muddle the attempt to solve the problem by analytical means which, in turn, necessitates some simplifying assumptions to obtain the solution. In this chapter, these assumptions will be linked to the definition of the three-dimensional thin wing problems.
This is a preview of subscription content, log in via an institution to check access.
eBook EUR 117.69 Price includes VAT (France)
Hardcover Book EUR 158.24 Price includes VAT (France)
Tax calculation will be finalised at checkout
Purchases are for personal use only
In the expression of Biot and Savart law for calculating the induced velocity, if we curl our fingers from the line segment \(\left( \overrightarrow<\mathrm
In Cartesian space, suppose a general ellipse is defined by the equation \(\frac>>+\frac>>=1\) , where a and b are the lengths of semi-major and semi-minor axes, respectively. The area enclosed by this ellipse will be \(\pi ab\) .
The properties associated with an airfoil section which are indeed the same as the properties of a wing of infinite span. These properties are different for the wings of finite span attached to a real aircraft. This is because, unlike an airfoil which is a two-dimensional object, a wing is essentially a three-dimensional body, that is, there will be a component of flow in the spanwise direction. That is, the flow over the wings is three-dimensional in nature and hence their aerodynamic properties are quite different from those of its airfoil sections.
The downwash produced by shedding trailing edge vortices from the wing tips and its effect on the inclination of the local relative wind has two major consequences on the local airfoil section. The actual angle of attack as seen by the airfoil locally is, in fact, lower than the geometric angle of attack \(\mathrm <\left( \alpha \right) >\) . This angle of attack is referred to as effective angle of attack \(\mathrm <\left( \alpha _
Also, the effective freestream velocity \(\mathrm <\left( U_
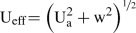
However, for small downwash \(\mathrm <\left( w\approx 0\right) >\)
$$\beginBesides, the downwash induced by these trailing edge vortices from the wing tips leads to an additional component of drag known as induced drag.
The concepts of vortex sheets and vortex filaments are advantageous in evaluating the aerodynamic characteristics of wings of finite span. From a directed line segment \(\mathrm <\left( dl\right) >\) of a vortex filament, the induced velocity can be calculated by using the below mentioned Biot–Savart law.
The velocity induced by a straight vortex filament of the finite length is given as
$$\beginIn the lifting line model, developed by Ludwig Prandtl, a wing is numerically described by an infinite number of horseshoe vortices and these bound vortices pass through the aerodynamic centers of the airfoils, which in turn creates the lifting line. Besides, the trailing edge vortices starting at the lifting line and shed downstream toward the infinity are basically responsible for inducing the downwash at the lifting line, and consequently, modify the local angles of attack. The circulation distribution \(\mathrm \) is calculated from the accompanying relation
For the symmetric aerodynamic load distribution, defined as \(\mathrm \left[ 1-\left( \frac\right) ^\right] ^>>\) , a summary of important relations is described below.
For a symmetric elliptical lift distribution over the wingspan, both induced downwash and induced angle are constant along the span.
$$ \mathrmThe total lift acting on the complete wingspan for a symmetric elliptic lift distribution is
$$\beginand the expression for \(\mathrm >\) is
$$\beginThe overall induced drag for a symmetric elliptical loading is given by
$$\beginIn addition, the coefficient of induced drag is
$$\beginThis relation can also be written as
$$\beginwhere \(\mathrm >>\) is the aspect ratio of a finite wing.
For the symmetric general aerodynamic load distribution, given by , a summary of important relations is described as follows.
The generalized expression for the induced angle \(\mathrm <\left( \alpha _\right) >\) is
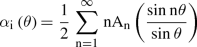
For a wing of finite span, the lift coefficient is given by
$$\beginand the coefficient of induced drag is
$$\begin© 2019 Springer Nature Singapore Pte Ltd.
Kaushik, M. (2019). Finite Wing Theory. In: Theoretical and Experimental Aerodynamics. Springer, Singapore. https://doi.org/10.1007/978-981-13-1678-4_6
Anyone you share the following link with will be able to read this content:
Get shareable link
Sorry, a shareable link is not currently available for this article.
Copy to clipboard
Provided by the Springer Nature SharedIt content-sharing initiative